Research
Pattern Control and Forecasting
Forecasting the future state of a system is a central goal in physics. Chaos can be a limiting factor in achieving this goal. One well-known example is weather, illustrated by the so-called butterfly effect: the idea that a small disturbance can be amplified to create large-scale changes to a system. We are investigating the role of instability in limiting predictive ability by using pattern control in a paradigm of pattern forming systems, Rayleigh-Bénard convection (RBC).
RBC exhibits complex spatial and temporal dynamics but is accessible experimentally and thus is an ideal system for laboratory study. A novel experimental technique of optical actuation provides us with an additional tool for probing system dynamics. This tool allows us to impose reproducibly a given convection pattern, e.g., a pattern near instability (specifically, the Skew-Varicose instability of the straight-roll pattern).

Selected perturbations are applied to an ensemble of these (nearly identical) patterns and decay lifetimes are measured as the system relaxes to the base state. We find that decay lifetimes increase near the instability and give a quantitative measure of distance from instability. A decomposition method we are developing constructs the eigenmodes and associated growth rates from the ensemble of pattern evolutions.
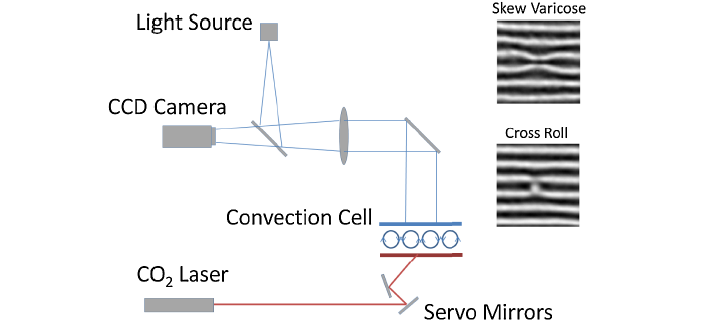
We also create patterns that undergo the instability, giving a set of systems evolving from nearby initial conditions on both sides of the instability boundary. This set can be used to test systematically the sensitivity of state estimation, a crucial process in forecasting. These studies will build upon an earlier application of a state estimation algorithm (the Local Ensemble Kálmán Transform Filter) to RBC which tested the ability of extracting state and parameter estimates from patterns exhibiting chaotic dynamics.
Below are two videos of systems prepared in similar initial target patterns using laser actuation which are then released and allowed to go unstable. Initially, their behavior is very similar but as time progresses their phase space trajectories diverge.
Representative Publications
- A.C. Perkins, R.O. Grigoriev, and M.F. Schatz, "Modal Spectra Extracted from Nonequilibrium Fluid Patterns in Laboratory Experiments on Rayleigh-Bénard Convection," Phys. Rev. Lett. 107, 064501 (2011).
- M. Cornick, B. Hunt, E. Ott, H. Kurtuldu, and M.F. Schatz, "State and parameter estimation of spatiotemporally chaotic systems illustrated by an application to Rayleigh-Bénard convection," Chaos 19, 013108 (2009).
- N. Garnier, R.O. Grigoriev, and M.F. Schatz, "Optical manipulation of microscale fluid flow," Phys. Rev. Lett. 91, 054501 (2003).
© 2013 Schatz Pattern Formation and Control Lab | Last updated: 12-10-2013
